中的应用。通过使用具有数字预失真 （DPD） 的 RF 发射器作为示例系统，并介绍了这个复杂系统的详细

　　射频 （RF） 和微波世界在很大程度上不受摩尔定律的严格约束，而数字世界中的积极扩展几十年来一直是常态。但现在，由于CMOS晶体管具有数十到数百GHz的皮秒开关速度和转换频率，因此有机会在单个集成电路上将射频和微波组件集成到一个完整的系统中。用于无线局域网和家庭基站的单已经成为商业现实。与复杂的数字系统一样，对一次通过设计成功的需求要求为整个系统的子系统组件提供准确的预测模型，从而能够在将设计提交到硬件之前对系统设计进行仿真并纠正任何错误或故障。这将节省时间和不必要地制造和测试整个系统的成本。

　　近年来，射频和微波设计的系统级建模和仿真变得非常复杂。AWR 和 Agilent 等EDA供应商现已提供具有广泛信号源、组件模型和数据分析工具库的商业仿真工具。射频和微波组件（如放大器和混频器）的非线性行为模型的开发，以及在典型应用环境中准确测量这些子系统的能力，是最近这些模拟器进步的重要推动因素。

　　本教程介绍了射频和微波子系统组件的系统级表征和建模技术，并说明了它们在混合信号、混合模式系统级仿真中的应用。我将使用具有数字预失真（DPD）的RF发射器作为示例系统，如图1所示。这是一个复杂的系统，包括：

　　预失真器的数字组件，可以实现为现场可编程门阵列 （FPGA） 或定制IC，而这些组件又可以通过高级描述语言（如Verilog）的模型进行描述，或者通过使用数学语言（如MathworksMATLAB软件）的算法函数来描述。

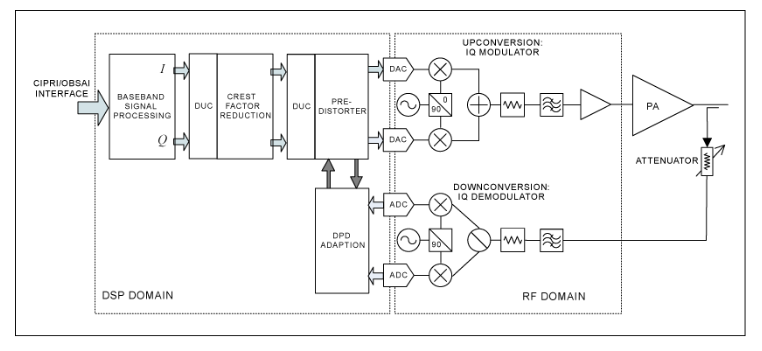
　　图 1.具有DPD功能的无线基础设施发射机系统的框图和DPD接收机的观察路径。该图显示了我们将要考虑的主要模块和仿真域

　　具有数字预失真 （DPD） 的射频发射器是实用复杂系统的一个很好的例子。通常，在这样的系统中，独立的团队将设计子系统组件，但重要的是要知道这些组件将作为一个完整的系统协同工作，最好是在硬件用螺栓连接在一起之前。这将使我们能够在设计阶段进行任何必要的架构更改，而不是在硬件构建之后。

　　我们需要一个能够控制多个不同模拟器引擎并处理它们之间的数据传输的仿真环境。例如，我们可以对系统的射频组件使用谐波平衡或包络瞬态仿真，而系统的数字部分将以时间步长或时间行进的方式进行仿真。我们可能还必须在不同的模拟器中管理浮点和定点数据表示。拥有一个可以管理这种协同仿真的模拟器工具是必不可少的。

　　在详细介绍模型、模型结构及其在仿真工具中的使用之前，我们先简要回顾一下在此类支持 DPD 的射频发射器系统中遇到的一些设计挑战和注意事项。虽然设计高功率射频放大器以满足宽带CDMAWCDMA）和长期演进（LTE）等现代频谱高效数字调制通信信号的功率和效率要求已经足够具有挑战性，但DPD的加入带来了一两个额外的皱纹。

　　WCDMA 和 LTE 等现代数字调制无线通信信号旨在最大限度地提高在给定带宽内可以传输的数据量。现代无线通信数字调制的细节可以在[3]中找到。除了调制和编码方案的复杂性外，这些信号最明显的特征之一是它们具有非常高的峰均功率比（PAPR），在实际情况下介于6dB至10dB之间。换句话说，信号峰值的功率可能比我们想要传输的信号的平均功率高 10 倍。平均功率决定了传输的范围;峰值功率决定了功率放大器的“尺寸”。这意味着放大器必须具有基站覆盖区域所需功率能力的 4 到 10 倍，才能处理峰值。从其峰值容量“后退”运行 AB 类 PA 通常意味着以非常低的效率运行，这是不可接受的，因为运行它的电力成本很高。相反，我们发现像Doherty这样的高效PA架构被用于无线基础设施基站PA。虽然效率很高，但这些功率放大器在以必要的高功率运行时会产生高水平的失真。因此需要某种形式的线性化技术，而DPD是目前的首选方法。

　　使用 DPD 会带来挑战。首先，我们需要在发射机中建立一条观察路径（见图1），以检测PA产生的失真。预失真器将PA输出与所需信号进行比较，然后使用非线性函数在PA输入信号中产生失真，使PA的输出成为所需信号的复制品。该非线性函数的参数不断调整，以最小化输入信号和PA输出之间的差异。这是一个控制系统。预失真器抵消了PA增益的压缩特性，因此它是一个扩展函数。在频域中，我们看到互调和邻道泄漏功率由DPD补偿。我们可以将其视为预失真器在PA输入中添加频率分量以抵消这些失真产物。有关DPD如何操作的更多详细信息，请参阅[4]。

　　将DPD添加到发射器的结果是，预失真信号的带宽比原始数据带宽宽得多;宽度最多五倍是常见的准则。这意味着从DPD算法到DAC和RF部分的发射链必须具有宽带宽。对于载波聚合可产生100MHz信号带宽的LTE而言，这是一个重大的设计和实现挑战。观测路径也应具有此带宽，以便能够捕获PA为DPD系统产生的高阶失真产物。此外，观察路径需要比发射机的其余部分更线性，因为就DPD而言，这里引入的任何失真都与PA产生的失真无法区分，并且由此产生的校正信号实际上会在PA输出中引入失真。观察路径需要低噪声和高动态范围，以便能够辨别低电平失真产物。这些都是重大的设计挑战，并增加了变送器的复杂性和成本。

　　在过去的二十年中，关于开发非线性射频和微波元件的行为模型已经取得了相当多的工作[5,6]。最近的重点特别放在PA建模上，因为该器件是典型发射机系统中非线性的主要来源。在此期间，识别所谓的“记忆效应”已成为发射机系统建模中最重要的挑战之一。例如，虽然使用多项式模型可以相当直接地对非线性进行建模，但包含记忆效应会使我们的建模和仿真任务变得非常复杂。

　　射频行为建模有两种主要方法：频域和时域。我们将概述这两种风格。非线性模型通常基于被测系统围绕某个工作点（例如直流条件或平均射频功率）的线性化。任何更通用的东西都太复杂了，无法构建和实现，并且不会简化我们的建模挑战。

　　频域是射频和微波工程师的天然家园。自 Kurokawa 的原始论文 [7] 以及 1960 年代引入矢量网络分析仪以来，我们一直在使用 S 参数进行线 年。因此，这种方法很受欢迎。

　　X参数模型[8]及其相关和相似的模型结构S函数[9]和“Cardiff”模型[10]是目前流行的现代频域模型。这些模型都基于围绕单个大音调（例如，PA的大信号驱动）的非线性响应的线性化。然后，通过测量对大音调外施加的小谐波信号的散射响应，在频域中探测非线性行为。Verspecht 和 Root 在本杂志 [11] 中清楚地解释了基本原理和数学基础。X 参数模型仅使用一阶导数来模拟非线性行为。这是一种相当优雅的方法，因为一阶导数是由雅可比算法中的模拟器自动计算的，它用于收敛到解，因此该模型简单快捷。S 函数以类似的方式运行，但也可以将DC条件作为显式建模变量包括在内。Cardiff 模型通过在模型中包含高阶导数来扩展 X 参数，这与泰勒级数一样，扩展了模型的有效区域并使其更具通用性。

　　X 参数的价值不仅在于模型公式，还在于构建它们的数据可以使用现成的设备进行测量，例如 AgilentPNA-X 非线性矢量网络分析仪。该仪器还可以构建与 AgilentADS 模拟器兼容的 X 参数模型文件。在PNA-X周围设置外部测量系统时，高功率PA确实需要格外小心，但这可以扩展仪器测量输出功率超过100W的PA上的X参数的能力[12]。我们还可以从仿真中生成电路的 X 参数描述。这意味着我们可以以相当直接的方式创建电路或子系统的非线性模型，甚至在设计过程的早期，用于更高级别的系统仿真。

　　X参数方法的一个缺点是这些模型在构造上是无记忆的，尽管最近有关于如何使用基于非线性积分模型的Volterra级数方法将长期和短期记忆效应纳入X参数模型结构的报道[13]。可以使用脉冲技术来测量记忆效应，以观察瞬态行为，并使用 [5]，第 3 章中描述的 NIM 方法提取记忆模型参数。内存组件通过乘积项包含在 X 参数公式中。由于长期记忆效应通常是偏置电源元件和PA夹具中偏置线设计的结果，这表明可以将这些电路效应建模为一个单独的模型元件，该元件可以“添加”到晶体管的X参数模型中，以产生完整的PA模型。

　　非线性动力学现象的自然归宿是时域，因为我们可以捕获瞬态，从而捕获能量存储或记忆效应，以及稳态行为。在射频和微波电路中使用时域数据的一个重大历史缺点是，测量的采样率必须非常高，导致采样不足或时间跨度较短的数据集。仿真中也出现了类似的问题：瞬态仿真的时间步长必须非常短，导致仿真时间很长。如今，这些问题已基本得到解决。最近，人们发布了带宽超过60GHz的实时采样示波器，能够使用高达50Gbps的信号进行表征[14]。包络瞬态仿真技术的发展使得在可控的时间内使用调制射频和微波信号对电路进行仿真成为可能。

　　蜂窝通信中使用的PA通常是相当窄的频带，输出匹配网络滤波器会衰减任何谐波。当这种PA被压缩时，被压缩的是信号的包络，而不是载波信号，它保持正弦波（实际上可能没有明确存在）。这意味着PA的非线性特性可以完全由包络行为来描述。我们可以使用包络，或者更准确地说，使用调制信号来表征PA：数据捕获的时间尺度现在处于调制速率。我们还可以使用包络瞬态仿真来描述调制信号如何受到PA非线性的影响。因此，我们的PA时域模型可以在调制速率下构建，而不是在微波频率下构建。

　　现代蜂窝通信中使用的数字调制通常以同相 （I） 和正交 （Q） 分量的形式创建。将 I 和 Q 组合在一起以产生所需的调制信号，通常是某种形式的正交相移密钥 （QPSK） 或幅度调制 （QAM）。时域 I 和 Q 数据可以在 PA 的输入和输出端进行测量或仿真，并在 AM-to-AM 或增益响应和 AM-to-PM（相位）响应中观察到非线性和存储器行为，如图 2 所示。从这些图中可以看出增益压缩和相位失真的总体趋势，以及响应在某个平均响应周围的“云”形式。正是这种云表明存在记忆效应。如果不存在记忆效应，这两个响应将是单行的，即“瞬时”响应。云层告诉我们的是，给定输出功率下的增益不仅取决于该时刻的输入功率，还取决于信号在前一个时间的值：它的历史。并非云中的每个点都具有完全相同的历史记录。

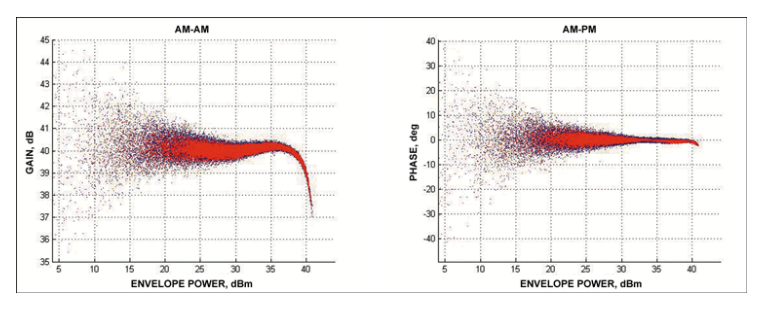
　　图2.功率放大器输入输出IQ数据的幅度和相位的AM至AM和AM至PM图。蓝点是测量数据，红点是简化的 Volterra 模型预测。

　　我们可以使用众所周知的非线性数据或函数拟合技术，通过AM-to-AM和AM-to-PM特性拟合曲线来构建PA模型。从本质上讲，我们试图将已知函数拟合到数据中。也许最流行和最简单的技术是多项式拟合数据。在实践中，这通常使用“最小二乘法”来完成，这种方法可以最小化函数和数据之间的平均欧几里得距离。通过构建多项式模型，我们基本上将泰勒级数展开拟合到数据中。

　　但这个过程会产生一个瞬时模型，无法捕捉到记忆效应。我们需要一个模型函数，在其公式中明确包含时域信号的历史。Volterra 系列来救援。Volterra 系列可用于模拟时不变非线性动力系统;换句话说，一个具有内存的非线性系统。Volterra 级数可以被认为是具有记忆的泰勒级。

上一篇:5G中RRC连接建立的两种机制
下一篇:射频器件概述和制造工艺